He doesn'tDoes he arrive at the correct result, given the inputs, or does he not? It's a simple question.
Cordially, Bernard
He doesn'tDoes he arrive at the correct result, given the inputs, or does he not? It's a simple question.
Using the same inputs, what do you believe is the mathematically correct result?Bernard Muller wrote:to Peter,He doesn'tDoes he arrive at the correct result, given the inputs, or does he not? It's a simple question.
For sure, I would use the addition law of probability, or the sum rule for the consequent odds:Using the same inputs, what do you believe is the mathematically correct result?
I am not going to make calculations (but you can, if you want). That would be a waste of time considering I would be channelled into having to deal with garbage input data and dubious categories.Another important property is:
P(A \cup B) = P(A) + P(B) - P(A \cap B).
This is called the addition law of probability, or the sum rule. That is, the probability that A or B will happen is the sum of the probabilities that A will happen and that B will happen, minus the probability that both A and B will happen.
Note: the math sign for \cup looks like a "U" and the math sign for \cap looks like a "U" reversed.
So this stuff...Bernard Muller wrote:to Peter,For sure, I would use the addition law of probability, or the sum rule for the consequent odds:Using the same inputs, what do you believe is the mathematically correct result?I am not going to make calculations (but you can, if you want). That would be a waste of time considering I would be channelled into having to deal with garbage input data and dubious categories.Another important property is:
P(A \cup B) = P(A) + P(B) - P(A \cap B).
This is called the addition law of probability, or the sum rule. That is, the probability that A or B will happen is the sum of the probabilities that A will happen and that B will happen, minus the probability that both A and B will happen.
Note: the math sign for \cup looks like a "U" and the math sign for \cap looks like a "U" reversed.
I have some details here:
viewtopic.php?f=3&t=1317&p=30320&hilit=hebrews#p30320
Cordially, Bernard
Yikes... This is just absurd. We've gone round in a circle, and your understanding is none improved for the trip.But even if we have 4 cases in favor of h, each one rated at only 30 %, the total will come to a probability of 76 %.

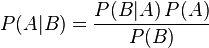
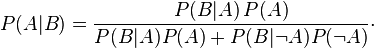
Play with dices. You'll get to the same result. OK, dices have 6 sides. let's say that 1 and 6 are TRUE. That's 33.33333% to be TRUE.Bernard wrote:Yikes... This is just absurd. We've gone round in a circle, and your understanding is none improved for the trip.But even if we have 4 cases in favor of h, each one rated at only 30 %, the total will come to a probability of 76 %.
h = testimony is accurate, e1 = first witness, e2 = second witness, e3 = third witnessBernard Muller wrote:to Peter,Play with dices. You'll get to the same result. OK, dices have 6 sides. let's say that 1 and 6 are TRUE. That's 33.33333% to be TRUE.Bernard wrote:Yikes... This is just absurd. We've gone round in a circle, and your understanding is none improved for the trip.But even if we have 4 cases in favor of h, each one rated at only 30 %, the total will come to a probability of 76 %.
Roll four dices together many times: 80% of the time, one of the four dices will come with a 1 or a 6.
That's according to the addition law of probability, or the sum rule.
OK, let's say you trust someone at 50% to tell the truth on a particular happening.
(let say he/she saw the suspect attacking the victim but it was from a long distance away, so the 50%)
You trust another person at 50% to tell the truth on the same matter.
(ditto)
These two persons do not know each other.
What are the chance of knowing the truth from these two persons. I say 0.50 + (0.50 x 0.50) = 0.75 => probability = 75%
Carrier would say: the odds for each is 1/1. (1/1 x 1/1) = 1/1 => probability = 50%
If we add a third person with 20% of saying the truth on the same thing (same circumstance but has his vision seriously deficient, so the 20%).
For me, that adds 5% (0.25 x 0.20) to the 75% for probability of 80%.
For Carrier 1/1 x 1/4 = 1/4 => probability of 20%
Cordially, Bernard
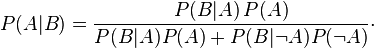
Carrier would say: the odds for each is 1/1. (1/1 x 1/1) = 1/1 => probability = 50%
No, a Bayesian analysis would have arrived at 5 out of 6 or 83.333%.For Carrier 1/1 x 1/4 = 1/4 => probability of 20%
The problem I see here is if P( h ) = 0.33333 then P( ~h ) = 0.66667P( h ) = 0.33333
P( ~h ) = 0.66667
P( e1 | h ) = 0.4608
P( e2 | h ) = 0.72
P( e3 | h ) = 1
P( e4 | h ) = 1
P( e1 | ~h ) = 1
P( e2 | ~h ) = 1
P( e3 | ~h ) = 1
P( e4 | ~h ) = .34722
Regarding:Bernard Muller wrote:In my example about the two witnesses, if they are deemed 50% right, that does not mean they are deemed wrong at 50%. The other 50% is just inconclusiveness, incertitude, not that these two witnesses saw others than the suspect and the victim.
This thead is about "Carrier's numbers and math in OHJ," as I recall. He wrote the book, so we should be trying to understand the Bayesian mathematical method, a valid and well-known technique that is employed in the book, and possibly criticizing its particular application here. There's a time and a place for everything. Carrier never claimed to do Mullerian mathematics. He claimed to do Bayesian mathematics.Bernard Muller wrote:In my example about
These are the prior probabilities assigned by Carrier. They must add up to 1. Mathematically must. No exceptions.Bernard Muller wrote:The problem I see here is if P( h ) = 0.33333 then P( ~h ) = 0.66667P( h ) = 0.33333
P( ~h ) = 0.66667